Rango intercuartil
La «mitad central» de los datos se encuentra entre el primer y el tercer cuartil.
El primer cuartil es el valor de los datos que separa el 25% inferior de los valores del 75% superior.
El tercer cuartil es el valor de los datos que separa el 75% inferior de los valores del 25% superior.
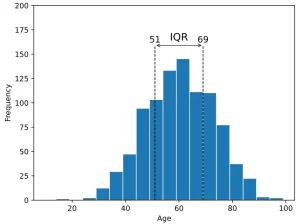
Este es un histograma de la edad de todos los 934 ganadores del Premio Nobel hasta el año 2020, mostrando el rango intercuartil (IQR):
La fórmula del rango intercuartil ayuda a encontrar la diferencia entre el tercer cuartil y el primer cuartil. La fórmula del rango intercuartil mide la variabilidad, basándose en la división de un conjunto ordenado de datos en cuartiles. Los cuartiles son tres valores o cortes que dividen cada parte respectiva como primer, segundo y tercer cuartil, denotados por
Q1, Q2 y Q3, respectivamente.
- Q1 es el corte de la primera mitad del conjunto de datos ordenados por rangos
- Q2 es el valor de la mediana del conjunto
- Q3 es el corte de la segunda mitad del conjunto de datos ordenados por rango.
Ejemplo
- Utilizando la fórmula del rango intercuartil, calcula el rango del siguiente conjunto de datos: {4, 17, 7, 14, 18, 12, 3, 16, 10, 4, 4, 11}
Solución: Dada: Número de términos = 12, Conjunto = {4, 17, 7, 14, 18, 12, 3, 16, 10, 4, 4, 11}
Conjunto ordenado = {3, 4, 4, 4, 7, 10, 11, 12, 14, 16, 17, 18}
Dividiendo el conjunto en cuartiles, cada cuartil tendrá 3 términos como: {3, 4, 4}, {4, 7, 10}, {11, 12, 14}, {16, 17, 18}
Primer cuartil,
Q1 = (4 + 4)/ 2 = 4
Tercer cuartil,
Q3 = (14 + 16)/2 = 15
Utilizando la fórmula del rango intercuartílico
Q2=Q3-Q1= 15 – 4
= 11
Por lo tanto, el rango intercuartil del conjunto dado = 11
- Determinar el valor del rango intercuartil de los diez primeros números impares.
Solución:
Hallar el IQR de los diez primeros números impares:
Los diez primeros números impares:1, 3, 5, 7, 9, 11, 13, 15, 17, 18
n = 10
Como 10 es par, utilizando la fórmula de la mediana, encontramos la mediana como la media de los términos 5 y 6.
Es decir
Q 2 = (9+11)/2 ⇒
Q 2 = 10.
Ahora
Q 1 es {1, 3, 5, 7, 9}
Aquí el número de puntos de datos = 5
Q 1 = mediana de {1,3,5,7,9} = 5
Q 3 parte es {11, 13, 15, 17, 19}
Aquí el número de puntos de datos = 5
Q 3 = mediana de {11,13,15,18,19} = 15
Utilizando la fórmula del rango intercuartil, IQR =
Q 3 – Q 1 Q 3 – Q 1
es 15 – 5 = 10
Respuesta: 10 es el rango intercuartil para el conjunto dado de los 10 primeros números impares.
Vídeos de Rango intercuartil
Contenido