Ecuacion de la hiperbola
Una hipérbola es un lugar de puntos de tal manera que la distancia a cada foco es una constante mayor que uno. En otras palabras, es el lugar de un punto que se mueve en un plano de tal manera que la relación entre su distancia a un punto fijo (foco) y la de una línea fija (directriz) es una constante mayor que 1.
Ecuación estándar de la hipérbola
La ecuación de la hipérbola es más sencilla cuando el centro de la hipérbola está en el origen y los focos están en el eje x o en el eje y. La ecuación estándar de una hipérbola viene dada por
[(x2 / a2) – (y2 / b2)] = 1donde , b2 = a2 (e2 – 1)
Términos y fórmulas importantes de la hipérbola
Hay ciertos términos relacionados con la hipérbola que deben ser entendidos a fondo para poder tener confianza con este concepto. Algunos de los términos más importantes relacionados con la hipérbola son
Excentricidad (e): e2 = 1 + (b2 / a2) = 1 + [(eje conjugado)2 / (eje transversal)2]
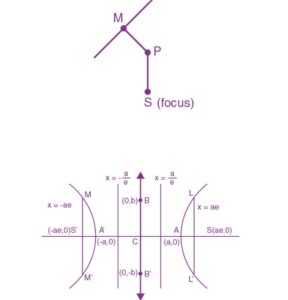
Focii: S = (ae, 0) & S′ = (-ae, 0)
Directriz: x=(a/e), x = (-a / e)
Eje transversal:
El segmento vivo A’A de longitud 2a en el que se encuentran los focii S’ y S se llama eje transversal de la hipérbola.
Eje conjugado:
El segmento de línea B’B de longitud 2b entre los 2 puntos B’ = (0, -b) & B = (0, b) se llama eje conjugado de la hipérbola.
Ejes principales:
El eje transversal y el eje conjugado.
Vértices:
A = (a, 0) & A’ = (-a, 0)
Cuerda focal:
Una cuerda que pasa por un foco se llama cuerda focal.
Doble ordenada:
La cuerda perpendicular al eje transversal se llama doble ordenada.
Latus Rectum:
La cuerda focal ⊥r al eje transversal se llama latus rectum.
Su longitud = (2b2 / a) = [(conjugada)2 / transversal] = 2a (e2 – 1)
La diferencia de las distancias focales es una constante
es decir, |PS-PS′| = 2a
Longitud del latus rectum = 2 e × (distancia del foco a la directriz correspondiente)
Puntos extremos del L.R : (± ae, ± b2 / a)
Centro:
El punto que biseca toda cuerda de la cónica, trazada a través de ella, se llama centro de la cónica.
C: (0, 0) es el centro de [(x2 / a2) – (y2 / b2)] = 1
Vídeos de Ecuacion de la hiperbola
Contenido