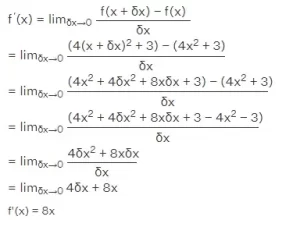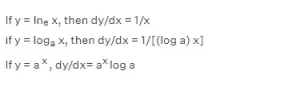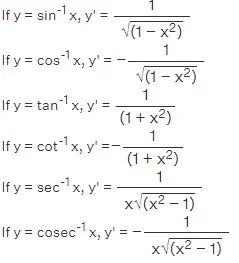Tabla de derivadas
Si f(x) es una función diferenciable en un intervalo [a,b], en cada punto del intervalo la derivada de la función existe finitamente y es única. Existe una nueva función g: [a,b] → R, tal que, x ∈ [a,b], g(x) = f'(x). Esta f'(x) es la primera derivada de la función f(x), que se denota por o Df(x) o f'(x).
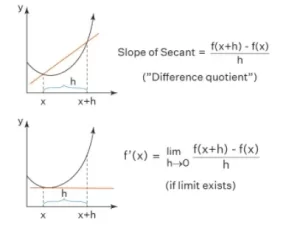
Consideremos una curva de la función f(x). Consideremos dos puntos (x, f(x)) y ((x+ h), f(x+h)). Entonces la pendiente de la recta secante que pasa por estos puntos viene dada por . Para obtener la pendiente real del punto, utilizamos el proceso de limitación de encontrar la derivada o pendiente del segundo punto por una variable «h». Intentamos calcular el cociente cuando h se acerca a 0. A medida que h se acerca a 0, el segundo punto se acerca al punto original y la recta secante se convierte en la recta tangente.
¿Cómo encontrar las derivadas?
Las derivadas se obtienen aplicando los límites según el primer principio de diferenciación que obtuvimos como definición de una derivada. Sea f(x) = 4×2 + 3
Por tanto, la primera derivada de 4×2 + 3 = 8x.
Así pues, la primera derivada de una función algebraica se obtiene utilizando la definición de la derivada.
Derivadas de funciones elementales
Las tres derivadas básicas de las funciones algebraicas, logarítmicas/exponenciales y trigonométricas se derivan del principio fundamental de la diferenciación y se utilizan como fórmulas de derivación estándar. Son las siguientes:

Derivadas de funciones trigonométricas
Si y = sen x, y’ = cos x
Si y = cos x, y’ = -sin x
Si y = tan x, y’ = sec2 x
Si y = sec x, y’ = sec x tan x
Si y = cosec x, y’ = -cosec x cot x
Si y = cot x, y’ = -cosec2 x
Derivadas de funciones trigonométricas inversas
Derivadas de funciones compuestas
Si f y g son funciones derivadas en su dominio, entonces f(g(x) también es diferenciable. Esto se conoce como la regla de la cadena de diferenciación utilizada para las funciones compuestas. (niebla)'(x) = f'[(g(x)] g'(x). Esto también se puede escribir como y = f(u) y t = g(x) , entonces dy/dx = dy/ dt . dt/dx
Por ejemplo, considera y = tan2x. Se trata de una función compuesta. Por la regla de la cadena, y = u2 , donde u = tan x
du/dt = 2u
dy/du = d/dx .tan x = sec 2 x
dy/dx = dy/du . du/dx
= 2 u . sec 2 x
= 2 tan x. sec 2 x
Vídeos de Tabla de derivadas
Contenido