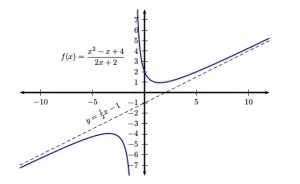
Asintota oblicua
Una asíntota es una línea recta que se aproxima constantemente a una curva dada pero que no se encuentra a ninguna distancia infinita. En otras palabras, la asíntota es una línea a la que se aproxima una curva a medida que se mueve hacia el infinito.
Dado que todas las rectas no verticales pueden escribirse de la forma y = mx + b para unas constantes m y b, decimos que una función f(x) tiene una asíntota oblicua y = mx + b si los valores (las coordenadas y) de f(x) se acercan cada vez más a los valores de mx + b a medida que se traza la curva hacia la derecha (x → ∞) o hacia la izquierda (x → -∞), es decir, si existe una buena aproximación,
f(x) ≈ mx + b,
Como puedes ver, la función (mostrada en azul) parece acercarse a la línea de puntos. Por tanto, la asíntota oblicua de esta función es y = ½ x – 1.
Cómo encontrar las asíntotas oblicuas
Una función puede tener como máximo dos asíntotas oblicuas, pero sólo se espera que ciertos tipos de funciones tengan una asíntota oblicua. Por ejemplo, los polinomios de grado 2 o superior no tienen asíntotas de ningún tipo. (Recuerda que el grado de un polinomio es el exponente más alto de cualquier término. Por ejemplo, 10×3 – 3×4 + 3x – 12 tiene grado 4).
Como aplicación rápida de esta regla, puedes decir con seguridad sin ningún trabajo que no hay asíntotas oblicuas para la función cuadrática f(x) = x2 + 3x – 10, porque es un polinomio de grado 2.
Por otro lado, algunos tipos de funciones racionales sí tienen asíntotas oblicuas.
Así que cuando veas una pregunta en el examen de Cálculo AB AP que pregunte por las asíntotas oblicuas, no lo olvides:
- Si la función es racional, y si el grado en la parte superior es uno más que el grado en la parte inferior: Usa la división de polinomios.
- Si la gráfica es una hipérbola con ecuación x2/a2 – y2/b2 = 1, entonces sus asíntotas serán y = ±(b/a)x. Otros tipos de hipérbolas también tienen fórmulas estándar que definen sus asíntotas.
Vídeos de Asintota oblicua
Contenido