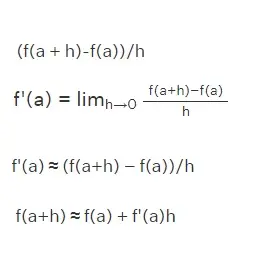Aplicaciones de la derivada
En matemáticas, las derivadas tienen un amplio uso. Se utilizan en muchas situaciones como encontrar los máximos o mínimos de una función, encontrar la pendiente de la curva, e incluso el punto de inflexión. A continuación se indican algunos lugares en los que utilizaremos la derivada. Y cada uno de ellos se explica en detalle en las siguientes secciones. El uso más común de la aplicación de las derivadas se ve en:
- Encontrar la tasa de cambio de una cantidad
- Encontrar el valor de aproximación
- Encontrar la ecuación de una Tangente y Normal a una Curva
- Encontrar los máximos y mínimos, y el punto de inflexión
- Determinación de funciones crecientes y decrecientes
Derivada para la Tasa de Cambio de una Cantidad
Las derivadas se utilizan para encontrar la tasa de cambio de una cantidad con respecto a la otra cantidad. Utilizando la aplicación de las derivadas podemos encontrar el cambio aproximado de una cantidad con respecto al cambio de la otra cantidad. Supongamos que tenemos una función y = f(x), que está definida en el intervalo [a, a+h], entonces la tasa media de cambio de la función en el intervalo dado es
Esto significa que si queremos encontrar el pequeño cambio en una función, sólo tenemos que encontrar la derivada de la función en el punto dado, y utilizando la ecuación dada podemos calcular el cambio. Por lo tanto, la derivada da la tasa de cambio instantánea de una función dentro de los límites dados y puede utilizarse para encontrar el cambio estimado en la función f(x) para el pequeño cambio en la otra variable(x).
Notas importantes sobre las aplicaciones de las derivadas
- La aplicación de las derivadas se utiliza para encontrar la tasa de cambios de una cantidad con respecto a la otra cantidad.
- La ecuación de la tangente y de la normal a una curva de una función se puede calcular utilizando las derivadas.
- La derivada de una función puede utilizarse para encontrar la aproximación lineal de una función a un valor dado.
Vídeos de Aplicaciones de la derivada
Contenido