Distribución normal fórmula
Todo tipo de variables en las ciencias naturales y sociales tienen una distribución normal o aproximadamente normal. La altura, el peso al nacer, la capacidad de lectura, la satisfacción en el trabajo o las puntuaciones de la selectividad son sólo algunos ejemplos de este tipo de variables.
Dado que las variables con distribución normal son tan comunes, muchas pruebas estadísticas están diseñadas para poblaciones con distribución normal.
Entender las propiedades de las distribuciones normales significa que puedes utilizar la estadística inferencial para comparar diferentes grupos y hacer estimaciones sobre poblaciones utilizando muestras.
¿Cuáles son las propiedades de las distribuciones normales?
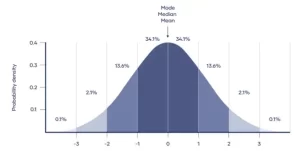
Las distribuciones normales tienen características clave que son fáciles de detectar en los gráficos:
- La media, la mediana y la moda son exactamente iguales.
- La distribución es simétrica con respecto a la media: la mitad de los valores están por debajo de la media y la otra mitad por encima.
- La distribución puede describirse mediante dos valores: la media y la desviación estándar.
- Media, mediana, moda y desviación estándar en una distribución normal
- La media es el parámetro de localización, mientras que la desviación típica es el parámetro de escala.
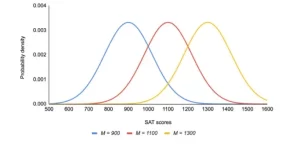
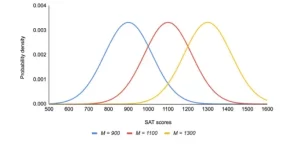
La media determina dónde se centra el pico de la curva. El aumento de la media desplaza la curva hacia la derecha, mientras que su disminución la desplaza hacia la izquierda.
Distribuciones normales con diferentes medias
La desviación estándar estira o aprieta la curva. Una desviación estándar pequeña da lugar a una curva estrecha, mientras que una desviación estándar grande conduce a una curva ancha.
Vídeos de Distribución normal fórmula
Contenido