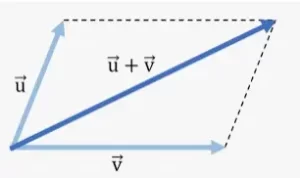
Método gráfico del paralelogramo
La ley del paralelogramo de la suma de vectores es un método que se utiliza para hallar la suma de dos vectores en la teoría vectorial. Estudiamos dos leyes para la suma de vectores: la ley del triángulo de la suma de vectores y la ley del paralelogramo de la suma de vectores. La ley del paralelogramo de la suma de vectores se utiliza para sumar dos vectores cuando los vectores que se van a sumar forman los dos lados adyacentes de un paralelogramo uniendo las colas de los dos vectores. Entonces, la suma de los dos vectores viene dada por la diagonal del paralelogramo.
La suma de dos vectores puede determinarse por adición vectorial y la ley del paralelogramo de la adición vectorial es una ley que facilita la determinación del vector resultante de la suma. Supongamos que un pez va de un lado a otro del río con el vector Q y que el agua del río fluye en una dirección con el vector P, como se muestra en la siguiente figura.
Ahora, la velocidad neta del pez será la suma de las dos velocidades – la velocidad del pez y la velocidad del flujo del río que será una velocidad diferente. Como resultado, el pez se moverá a lo largo de un vector diferente que será la suma de estas dos velocidades. Ahora, para determinar la velocidad neta, podemos considerar estos dos vectores como los lados adyacentes de un paralelogramo y utilizar la ley del paralelogramo de adición de vectores para determinar el vector suma resultante.
Fórmula de la Ley del Paralelogramo de la Suma de Vectores
Consideremos dos vectores P y Q con un ángulo θ entre ellos. La suma de los vectores P y Q viene dada por el vector R, el vector suma resultante utilizando la ley del paralelogramo de la adición de vectores. Si el vector resultante R forma un ángulo ϕ con el vector P, entonces las fórmulas para su magnitud y dirección son:
|R| = √(P2 + Q2 + 2PQ cos θ)
β = tan-1[(Q sin θ)/(P + Q cos θ)]
Enunciado de la ley del paralelogramo de la adición de vectores: Si dos vectores pueden ser representados por los dos lados adyacentes (tanto en magnitud como en dirección) de un paralelogramo trazado desde un punto, entonces su vector suma resultante está representado completamente por la diagonal del paralelogramo trazado desde el mismo punto.
Ahora, para demostrar la fórmula de la ley del paralelogramo, consideramos dos vectores P y Q representados por los dos lados adyacentes OB y OA del paralelogramo OBCA, respectivamente. El ángulo entre los dos vectores es θ. La suma de estos dos vectores está representada por la diagonal trazada desde el mismo vértice O del paralelogramo, el vector suma resultante R que forma un ángulo β con el vector P.
Prolongamos el vector P hasta D de forma que CD sea perpendicular a OD. Como OB es paralelo a AC, por lo tanto el ángulo AOB es igual al ángulo CAD ya que son ángulos correspondientes, es decir, el ángulo CAD = θ. Ahora, primero, derivaremos la fórmula para la magnitud del vector resultante R (lado OC).
En el triángulo rectángulo OCD, tenemos
OC2 = OD2 + DC2
⇒ OC2 = (OA + AD)2 + DC2 — (1)
En el triángulo rectángulo CAD, tenemos
cos θ = AD/AC y sin θ = DC/AC
⇒ AD = AC cos θ y DC = AC sin θ
⇒ AD = Q cos θ y DC = Q sin θ — (2)
Sustituyendo los valores de (2) en (1), tenemos
R2 = (P + Q cos θ)2 + (Q sin θ)2
⇒ R2 = P2 + Q2cos2θ + 2PQ cos θ + Q2sin2θ
⇒ R2 = P2 + 2PQ cos θ + Q2(cos2θ + sin2θ)
⇒ R2 = P2 + 2PQ cos θ + Q2 [cos2θ + sin2θ = 1]
⇒ R = √(P2 + 2PQ cos θ + Q2) → Magnitud del vector resultante R
A continuación, vamos a determinar la dirección del vector resultante. Tenemos en el trazado de la derecha ODC,
tan β = DC/OD
⇒ tan β = Q sin θ/(OA + AD) [De (2)]
⇒ tan β = Q sin θ/(P + Q cos θ) [De (2)]
⇒ β = tan-1[(Q sin θ)/(P + Q cos θ)] → Dirección del vector resultante R
Vídeos de Método gráfico del paralelogramo
Contenido