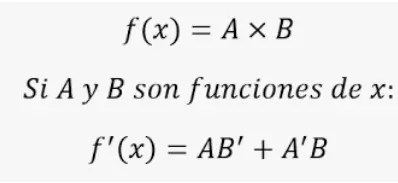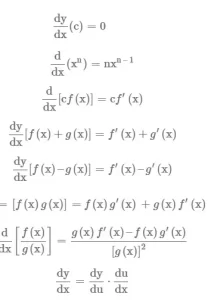Teorema de derivadas
Las tres derivadas básicas (D) son: (1) para funciones algebraicas, D(xn) = nxn – 1, en la que n es cualquier número real; (2) para funciones trigonométricas, D(sen x) = cos x y D(cos x) = -sin x; y (3) para funciones exponenciales, D(ex) = ex.
Para las funciones formadas por combinaciones de estas clases de funciones, la teoría proporciona las siguientes reglas básicas para diferenciar la suma, el producto o el cociente de dos funciones cualesquiera f(x) y g(x) cuyas derivadas se conocen (donde a y b son constantes): D(af + bg) = aDf + bDg (sumas); D(fg) = fDg + gDf (productos); y D(f/g) = (gDf – fDg)/g2 (cocientes).
La otra regla básica, llamada regla de la cadena, proporciona una forma de diferenciar una función compuesta. Si f(x) y g(x) son dos funciones, la función compuesta f(g(x)) se calcula para un valor de x evaluando primero g(x) y luego evaluando la función f en este valor de g(x); por ejemplo, si f(x) = sen x y g(x) = x2, entonces f(g(x)) = sen x2, mientras que g(f(x)) = (sen x)2. La regla de la cadena establece que la derivada de una función compuesta viene dada por un producto, ya que D(f(g(x))) = Df(g(x)) ∙ Dg(x). En palabras, el primer factor de la derecha, Df(g(x)), indica que primero se halla la derivada de Df(x) como es habitual, y luego se sustituye x, dondequiera que aparezca, por la función g(x). En el ejemplo de sen x2, la regla da el resultado D(sen x2) = Dsin(x2) ∙ D(x2) = (cos x2) ∙ 2x.
Teorema de Rolle
Si f(a) = f(b) entonces
existe un número real c ∈ (a, b) tal que f'(c) = 0, Este caso especial se llama teorema de Rolle.
El teorema de Rolle establece esencialmente que cualquier función diferencial de valor real que alcanza valores iguales en dos puntos distintos de la misma, debe tener al menos un punto estacionario en algún lugar entre ellos, es decir, un punto donde la primera derivada (la pendiente de la línea tangente a la gráfica de una función) es cero.
Vídeos de Teorema de derivadas
Contenido