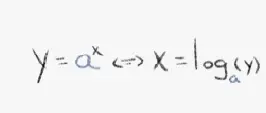Funciones trascendentes
En matemáticas, función no expresable como una combinación finita de las operaciones algebraicas de suma, resta, multiplicación, división, elevación a una potencia y extracción de una raíz. Los ejemplos incluyen las funciones log x, sin x, cos x, ex y cualquier función que las contenga. Tales funciones son expresables en términos algebraicos sólo como series infinitas. En general, el término trascendental significa no algebraico. Véase también número trascendental.
Funciones algebraicas y trascendentales
Las funciones trascendentales más conocidas son el logaritmo, la exponencial (con cualquier base no trivial), la trigonométrica y la hiperbólica, y las inversas de todas ellas. Menos conocidas son las funciones especiales del análisis, como las funciones gamma, elíptica y zeta, todas ellas trascendentes. Las funciones hipergeométricas generalizadas y de Bessel son trascendentes en general, pero algebraicas para algunos valores especiales de los parámetros.
Una función que no es trascendental es algebraica. Ejemplos sencillos de funciones algebraicas son las funciones racionales y la función raíz cuadrada, pero en general, las funciones algebraicas no pueden definirse como fórmulas finitas de las funciones elementales.
La integral indefinida de muchas funciones algebraicas es trascendental. Por ejemplo, la función logaritmo surgió de la función recíproca en un esfuerzo por encontrar el área de un sector hiperbólico.
El álgebra diferencial examina cómo la integración crea frecuentemente funciones que son algebraicamente independientes de alguna clase, como cuando se toman polinomios con funciones trigonométricas como variables.
Funciones trascendentales
La mayoría de las funciones trascendentales conocidas, incluidas las funciones especiales de la física matemática, son soluciones de ecuaciones diferenciales algebraicas. Las que no lo son, como las funciones gamma y zeta, se denominan funciones trascendentales o hipertrascendentales.
Análisis dimensional
En el análisis dimensional, las funciones trascendentales son notables porque sólo tienen sentido cuando su argumento es adimensional (posiblemente después de una reducción algebraica). Por ello, las funciones trascendentales pueden ser una fuente de errores dimensionales fácil de detectar. Por ejemplo, log(5 metros) es una expresión sin sentido, a diferencia de log(5 metros / 3 metros) o log(3) metros. Se podría intentar aplicar una identidad logarítmica para obtener log(5) + log(metros), lo que pone de manifiesto el problema: aplicar una operación no algebraica a una dimensión crea resultados sin sentido.
Vídeos de Funciones trascendentes
Contenido