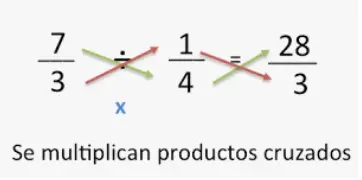
Fracciones de división
Sabemos que la división es un método para repartir equitativamente y poner en grupos iguales. Dividimos un número entero entre el divisor para obtener el cociente. Ahora bien, cuando hacemos la división de una fracción por otra fracción, es lo mismo que multiplicar la fracción por el recíproco de la segunda fracción. El recíproco de una fracción es una forma sencilla de intercambiar el numerador y el denominador de la fracción.
Dividir fracciones entre fracciones
Acabamos de aprender a dividir fracciones tomando el recíproco. Ahora, veamos el método de dividir fracciones entre fracciones con un ejemplo. Observa la fórmula de la división de una fracción por una fracción que se da a continuación. Si x/y se divide entre a/b, esto implica
x/y ÷ a/b
⇒ x/y × b/a (el recíproco de a/b es b/a)
⇒ xb/ya
Ahora, si necesitamos dividir 5/8 ÷ 15/16, sustituiremos los valores de los numeradores y denominadores dados.
5/8 ÷ 15/16 = 5/8 × 16/15 = 2/3
∴ El valor de 5/8 ÷ 15/16 = 2/3.
División de fracciones con números enteros
Para la división de fracciones con números enteros, necesitamos multiplicar el denominador de la fracción dada con el número entero dado. En la forma general, si x/y es la fracción y a es el número entero, entonces x/y ÷ a = x/y × 1/a = x/ya.
Dividir fracciones con decimales
Sabemos que los números decimales son una fracción en base 10. Podemos representar el decimal en la forma fraccionaria y luego realizar la división. Para dividir fracciones con decimales, sigue los pasos que se indican a continuación:
- Convertir el decimal dado en una fracción.
- Dividir ambas fracciones.
Consideremos el ejemplo 4/5 ÷ 0,5. Aquí, 0,5 puede escribirse en forma fraccionaria como 5/10 o 1/2. Ahora, divide 4/5 entre 1/2. Esto implica, 4/5 ÷ 1/2 = 4/5 × 2/1 = 8/5. Así es como realizamos la división de fracciones con decimales. Ahora vamos a aprender a dividir fracciones con números mixtos.
División de fracciones y números mixtos
Hemos aprendido a convertir fracciones mixtas en fracciones impropias. Para la división de fracciones con números mixtos, tenemos que convertir primero la fracción mixta en fracción impropia y luego dividirlas como dividimos dos fracciones. Consideremos el siguiente ejemplo.
3/4 ÷
Entonces, el primer paso es convertir a una fracción impropia. es lo mismo que 3/2. Ahora, se puede resolver de la siguiente manera:
3/4 ÷ 3/2
⇒ 3/4 × 2/3
⇒ 6/12 = 1/2
Por tanto, 3/4 ÷ = 1/2. Si quieres dividir un número mixto con una fracción, primero convierte el número mixto en una fracción impropia y sigue los mismos pasos indicados anteriormente
Vídeos de Fracciones de división
Contenido