Derivadas trigonométricas inversas

por
Derivadas trigonométricas inversas
Las derivadas trigonométricas inversas son las derivadas de las funciones trigonométricas inversas. Tenemos 6 funciones trigonométricas inversas que son las inversas de las 6 funciones trigonométricas básicas.

Derivadas trigonométricas inversas

¿Qué son las derivadas trigonométricas inversas?

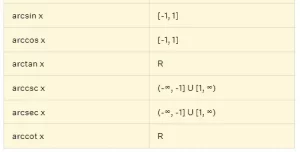
Las derivadas trigonométricas inversas son las derivadas de las funciones trigonométricas inversas arcsin (o sin-1), arccos (o cos-1), arctan (o tan-1), etc. Utilizamos la diferenciación implícita para encontrar las derivadas de la función trigonométrica inversa, que exploraremos en detalle en la próxima sección. Aquí están las derivadas trigonométricas inversas:

  • La derivada de arcsin x es d/dx(arcsin x) = 1/√1-x², cuando -1 < x < 1
  • La derivada de arccos x es d/dx(arccos x) = -1/√1-x², cuando -1 < x < 1
  • La derivada de arctan x es d/dx(arctan x) = 1/(1+x²), para todo x en R
  • La derivada de arccsc x es d/dx(arccsc x) = -1/(|x|√x²-1), cuando x < -1 o x > 1
  • La derivada de arcsec x es d/dx(arcsec x) = 1/(|x|√x²-1), cuando x < -1 o x > 1
  • La derivada de arccot x es d/dx(arcsin x) = -1/(1+x²), para todo x en R

Fórmulas de las derivadas trigonométricas inversas

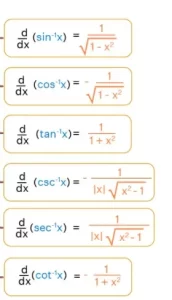
Ya hemos visto cuáles son las derivadas de las funciones trigonométricas inversas. Estas derivadas se pueden escribir en notación alternativa como sigue:

Ejemplos de derivadas trigonométricas inversas

  • ¿Cuál es la derivada de sen-1(2×3)?

Solución:

Por las derivadas de las funciones trigonométricas inversas,

d/dx (sin-1x) = 1/√1-x²

Usando esto y también la regla de la cadena

d/dx (sin-1(2×3)) = 1/√1-(2x³)² d/dx(2×3)

= 1/√1-4x⁶ (6×2)

Respuesta: La derivada de sin-1(2×3) es (6×2)/√1-4x⁶.

  • Hallar la derivada de sen-1x + cos-1x.

Solución:

Por las derivadas trigonométricas inversas,

d/dx (sin-1x) = 1/√1-x²

d/dx (cos-1x) = -1/√1-x²

Por tanto, d/dx (sen-1x + cos-1x)

= 1/√1-x² – 1/√1-x²

= 0

Respuesta: La derivada de sin-1x + cos-1x es 0.

  •  ¿Cuál es la derivada de x tan-1x?

Solución:

Por las fórmulas de la derivada trigonométrica inversa,

d/dx(tan-1x) = 1/(1+x²)

Por la regla del producto,

d/dx(x tan-1x) = x d/dx(tan-1x) + tan-1x d/dx(x)

= x/(1+x²) + tan-1x

Respuesta: La derivada de x tan-1x es x/(1+x²) + tan-1x.

Vídeos de Derivadas trigonométricas inversas

https://www.youtube.com/watch?v=ulwkT9cMDJ4

Contenido