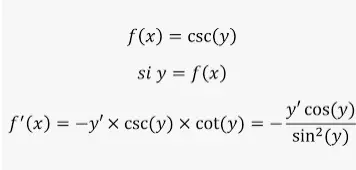Derivada de cosecante
La derivada de cot x con respecto a x se representa por d/dx (cot x) (o) (cot x)’ y su valor es igual a -csc2x. Cot x es una función diferenciable en su dominio. Para demostrar que la diferenciación de cot x es -csc2x, utilizamos las fórmulas trigonométricas y las reglas de diferenciación. Vamos a demostrar esta fórmula de las siguientes maneras:
- Prueba por primer principio
- Prueba por la regla de la cadena
- Prueba por la regla del cociente
Fórmula de la derivada de cot x
La fórmula de la diferenciación de cot x es
d/dx (cot x) = -csc2x (o)
(cot x)’ = -csc2x
La derivada de cot x es csc al cuadrado de x. Se denota como cot x elevado a d o d sobre d x de cot x.
Demostremos esto en cada uno de los métodos mencionados.
Derivada de cot x Prueba por primer principio
Para encontrar la derivada de cot x por primer principio, suponemos que f(x) = cot x. Por el primer principio (o definición de derivada), la derivada de f(x) viene dada por el siguiente límite
f'(x) = limₕ→₀ [f(x + h) – f(x)] / h … (1)
Como f(x) = cot x, tenemos que f(x + h) = cot (x + h).
Sustituyendo esto en (1)
f'(x) = limₕ→₀ [cot(x + h) – cot x] / h
= limₕ→₀ [ [cos (x + h) / sin (x + h)] – [cos x / sin x] ] / h
= lim→₀ [ [sin x cos(x + h ) – cos x sin(x + h)] / [sin x – sin(x + h)] ]/ h
Por fórmulas de suma y diferencia, sin A cos B – cos A sin B = sin (A – B).
f'(x) = limₕ→₀ [ sin (x – (x + h)) ] / [ h sin x – sin(x + h)]
= limₕ→₀ [ sin (-h) ] / [ h sin x – sin(x + h)]
Tenemos que sin (-h) = – sin h.
f'(x) = – limₕ→₀ (sin h)/ h – limₕ→₀ 1 / [sin x – sin(x + h)]
Por fórmulas de límite, limₕ→₀ (sin h)/ h = 1.
f'(x) = -1 [ 1 / (sin x – sin(x + 0))] = -1/sin2x
Sabemos que el recíproco de sin es csc. Por lo tanto
f'(x) = -csc2x.
Por tanto, queda demostrado.
Derivada de Cot x Prueba por la regla de la cadena
Podemos demostrar la fórmula de la derivada de cot x mediante la regla de la cadena. Para ello, recordemos que cot y tan son recíprocos entre sí. Así que podemos escribir y = cot x como y = 1 / (tan x) = (tan x)-1. Como aquí tenemos una potencia, podemos aplicar la regla de la potencia. Por la regla de la potencia y la regla de la cadena
y’ = (-1) (tan x)-2 – d/dx (tan x)
La derivada de tan x es, d/dx (tan x) = sec2x. Además, una de las propiedades de los exponentes dice, a-m = 1/am.
y’ = -1/tan2x – (sec2x)
y’ = – cot2x – sec2x
Ahora, cot x = (cos x)/(sin x) y sec x = 1/(cos x). Así que
y’ = -(cos2x)/(sin2x) – (1/cos2x)
= -1/sin2x
Sabemos que el recíproco de sin es csc. es decir, 1/sin x = csc x. Así que
y’ = -csc2x
Por tanto, queda demostrado.
Derivada de Cot x Prueba por la regla del cociente
Encontraremos la derivada de cot x utilizando la regla del cociente. Esta demostración es la más fácil entre todos los demás métodos para demostrar la derivada de cot x. Como la regla del cociente trata con derivadas de fracciones, escribiremos cot x como una fracción. Sabemos que cot x = (cos x)/(sen x). Así que suponemos que y = (cos x)/(sen x). Entonces, por la regla del cociente
y’ = [ sin x – d/dx (cos x) – cos x – d/dx (sin x)] / (sin2x)
= [sin x – (- sin x) – cos x (cos x)] / (sin2x)
= [-sin2x – cos2x] / (sin2x)
= -[sin2x + cos2x] / (sin2x)
Por una de las identidades pitagóricas, cos2x + sin2x = 1. Así que
y’ = -1 / (sin2x) = -csc2x
Por lo tanto, queda demostrado.
Conceptos erróneos comunes relacionados con la derivada de Cot x:
Aquí hay algunos conceptos erróneos comunes relacionados con la diferenciación de cot x. Vamos a aclarar.
- Aunque cot x = (cos x)/(sin x), d/dx (cot x) NO es igual a d/dx(cos x) / d/dx (sin x).
- Tenemos que utilizar la regla del cociente para encontrar la derivada de cot x (escribiéndola como (cos x)/(sin x)).
- d/dx (cot x) NO es tan x. Cot y tan son recíprocos entre sí.
- La derivada de cot x y la derivada de cot inversa a x NO son iguales.
- d/dx(cot x) = -csc2x
- d/dx(cot-1x) = -1/(1 + x2)
Vídeos de Derivada de cosecante
Contenido