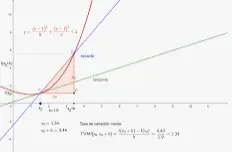
Tasa de variacion instantanea
Hay muchos otros usos del concepto de tasa de cambio instantánea. Los químicos lo utilizan para examinar las reacciones químicas. Los ingenieros eléctricos utilizan este concepto para describir los cambios que se producen en la corriente de un circuito eléctrico. Los economistas utilizan este concepto para describir los beneficios y las pérdidas de una empresa determinada.
Para entender el concepto de tasa de variación instantánea, primero es necesario comprender el significado de los términos tasa de variación media y límite.
Tasa de variación media
La tasa de variación media describe cómo cambia una variable cuando la otra aumenta en una sola unidad. Por ejemplo, Galileo descubrió que si se ignora el impacto de la resistencia del aire, la distancia que recorre un objeto
con respecto al tiempo cuando se deja caer desde una altura determinada se describe mediante la siguiente función:
s (t ) = 4,9t 2 donde t ≥ 0.
En esta función, t indica el tiempo transcurrido desde que se dejó caer el objeto. La evaluación de esta función, s (t ), describe la distancia total que ha recorrido el objeto en un momento dado. Por ejemplo, después de 2 segundos, el objeto habrá recorrido una distancia total de 4,9 (22) o aproximadamente 19,6 metros. Esto es, por supuesto, suponiendo que el objeto aún no haya tocado el suelo.
Para calcular la velocidad media de cambio descrita por la función s (t ), es útil examinar un gráfico de esta función. Para esta discusión, supongamos que el objeto se deja caer desde una altura de 240 metros. La gráfica de la función, s (t ), se muestra en (a) de la figura. Observa que la gráfica comienza en 0 segundos y termina en 7 segundos. La curva de esta gráfica sugiere que la velocidad del objeto cambia con el tiempo. Dado que este objeto se deja caer desde una altura de 240 metros (m), después de aproximadamente 7 segundos el objeto llegará al suelo (4,9 (72) = 240,1 m).
La velocidad media de cambio es la distancia media que se recorre en un solo segundo. Para determinar la velocidad media de cambio, se forma una relación entre la diferencia entre la distancia recorrida y el tiempo transcurrido. Esto puede expresarse como m/seg. Esta misma expresión algebraica puede utilizarse también para determinar la pendiente del segmento de línea entre los puntos (0, 0) y (7, 240). El segmento de línea coloreado en (a) de la figura tiene una pendiente de . La pendiente de esta línea representa la tasa de cambio promedio de la función s (t ). Una interpretación de esta pendiente es que en promedio el objeto cubre una distancia de metros cada segundo. Si la función original hubiera sido una línea recta, entonces la pendiente de esa línea sería igual a la tasa de cambio promedio de esa función.
Es importante reconocer en el ejemplo actual que es la tasa de cambio promedio para un intervalo de tiempo de 7 segundos. La tasa de cambio promedio también puede calcularse para intervalos de tiempo más pequeños. Por ejemplo, la tasa de cambio promedio puede ser calculada para cada intervalo de tiempo de 1 segundo. Estos cálculos se muestran en la primera tabla. Una representación gráfica del promedio
Vídeos de Tasa de variacion instantanea
Contenido