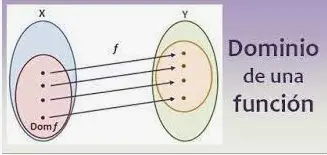
Cual es el dominio de una funcion
El dominio de una función son los números de entrada que, cuando se introducen en una función, se define el resultado. En palabras simples, podemos definir el dominio de una función como los posibles valores de x que harán que una ecuación sea verdadera.
Algunos de los casos que no harán una función válida son cuando una ecuación está siendo dividida por cero o una raíz cuadrada negativa.
Por ejemplo, f(x) = x2 es una función válida porque, independientemente del valor de x que se pueda sustituir en una ecuación, siempre hay una respuesta válida. Por esta razón, podemos concluir que el dominio de cualquier función son todos los números reales.
El rango de una función se define como el conjunto de soluciones de la ecuación para una entrada dada. En otras palabras, el rango es la salida o el valor y de una función. Sólo hay un rango para una función dada.
Indique el dominio y el rango de la siguiente relación. ¿Es la relación una función?
{(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}
La lista de puntos anterior, al ser una relación entre ciertas x y ciertas y, es una relación. El dominio son todos los valores de x, y el rango son todos los valores de y. Para dar el dominio y el rango, simplemente enumero los valores sin duplicar:
dominio: {2, 3, 4, 6}
rango: {-3, -1, 3, 6}
(Es habitual enumerar estos valores en orden numérico, pero no es necesario. Los conjuntos se llaman «listas desordenadas», así que puedes enumerar los números en el orden que quieras. Sólo no dupliques: técnicamente, las repeticiones están bien en los conjuntos, pero la mayoría de los instructores descontarían por esto).
Aunque el conjunto dado representa efectivamente una relación (porque las x y las y se relacionan entre sí), el conjunto que me dieron contiene dos puntos con el mismo valor de x: (2, -3) y (2, 3). Como x = 2 me da dos posibles destinos (es decir, dos posibles valores de y), entonces esta relación no es una función.
Indica el dominio y el rango de la siguiente relación. ¿Es la relación una función?
{(-3, 5), (-2, 5), (-1, 5), (0, 5), (1, 5), (2, 5)}
Sólo voy a enumerar los valores x para el dominio y los valores y para el rango:
dominio: {-3, -2, -1, 0, 1, 2}
rango: {5}
Vídeos de Cual es el dominio de una función
https://www.youtube.com/watch?v=c20QWEhBPKs
Contenido